Introduction
Home sweet home on the Direwolf20 1.16 server.
I have played a lot of Minecraft and continue to enjoy the game because it is very open ended and every world is unique. For those that don’t know, Minecraft is a world made of blocks, and all the blocks can be moved or changed by the player. It starts off as a procedurally generated “infinite” world for the player to explore and develop however they see fit. There is a lot of content in the vanilla game: monsters to fight, crops to grow, tools to build, etc. Minecraft also supports third party modifications which add new blocks with new functionality to the game. I tend to play on heavily modded minecraft servers (with 100+ mods), and the content decribed here was created on a Direwolf20 1.16 server, which adds a couple of orders of magnitude more complicated blocks to the vanilla game. A lot of these mods add content that turns Minecraft into more of a Logistics/4X game like Rimworld or Factorio (other favorites of mine).
But enough about why I like Minecraft; the focus of this post is really on cellular automatons and how a particular one, Rule 110, can be implemented in Minecraft. Automaton is the word computational theorists use to describe the most general form of machines able to perform logical operations. These abstract machines ignore the details of realizing (constructing) a machine that performs some logical operation, and focus specifically on the logic. As such, automaton theory is full of formal logic and proofs, which can hide what I consider to be really interesting and easy to grasp concepts that are the theoretical underpinning of the technological world we live in today. I’ll try to give an easy-to-digest introduction to why cellular automatons are interesting, and then get into the Minecraft implementation toward the end.
Universality and Automatons
The concept of Turing completeness essentially boils down to the idea that logic is independent of implementation. Said differently, any implementation able to perform some sufficient set of logical operations can be used to simulate (implement) any other implementation. So the universal Turing machine consisting of a tape with symbols (which it can change) and rules for what the machine does when it reads any particular symbol, is able to perform the same computations as your von Neumann architecture computer being used to read this. Granted, your modern computer will be more efficient and faster than any real Turing machine, but Turing completeness only claims that the class of machines are all functionally equivalent without setting any bounds on time taken to perform the computations.
All machines exhibiting Turing completeness are also automatons, but not all automatons are Turing complete. Typically the proof that a particular automaton exhibits the universality of Turing completeness is achieved by implementing (simulating) some known-complete machine with that automaton. This raises a conceptually interesting question: what is the simplest automaton that exhibits Turing completeness? It is now know that a Turing machine with 2 states and 3 symbols is universal. Like other Turing machines, it is conceptualized as a “head” reading a “tape” of three possible symbols. At any given time, the machine is in one of two possible states. Depending only on the state and symbol, the machine can:
- Modify the symbol
- Transition into a new state
- Move left or right to the next symbol
With 2 states and 3 symbols, there are 6 rules for what to do, and this is sufficient to implement any possible logical operation. Actually implementing useful logic in such a simple machine is the tricky part; these very simple machines can take many (many) steps and very large amounts of symbols to achieve even basic operations, but it is technically possible.
Universality and Cellular Automatons
Given that modern computers read lists of instructions and perform operations based on the instruction read, it’s not too much of a stretch to see how Turing machines with their tape readers and symbols may be equivalent. That said, modern computers and Turing machines (universal or not) are relatively difficult to implement. Turing machines require some tape reading/writing mechanism and a way to keep track of the states and rules associated with state transitions. Von Neumann computers require memory, registers, a whole suite of instructions, and associated buses to link them all together. It’s perhaps interesting to consider alternate forms of machines that may also be Turing complete, and cellular automatons fit the bill nicely.
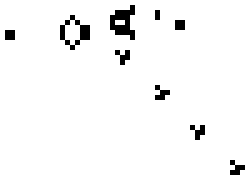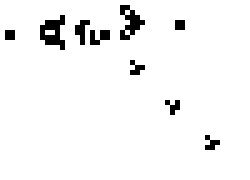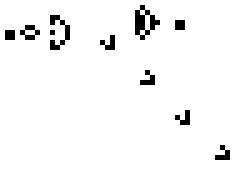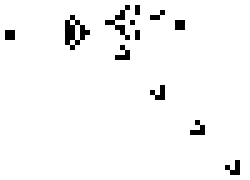
A glider generator in the Game of Life Johan G. Bontes CC BY-SA 3.0
Cellular automatons consist of (usually) simple automatons arranged such that each one has some number of neighboring, identical automatons. The most well known of these is probably Conway’s Game of Life (GoL) with automatons arranged on a 2D grid, where only the eight nearest neighbors interact. All automatons on the grid transition to a new state at the same time according to a simple set of rules:
- Any active automaton with two or three active neighbors remains active.
- Any inactive automaton with three live neighbors becomes active.
- All other automatons become inactive.
This can lead to exceptionally complex behavior (see GIFs on the Wikipedia page linked above), and, most importantly, persistent traveling patterns known as “gliders” or “spaceships” (seriously). The way these traveling patterns interact is where the computational power lies: intersecting gliders can cancel each other out, or not, depending on precisely how they collide. Using this, streams of gliders can be used to construct basic logic gates, from which any computation can be derived. Indeed a von Neumann machine has been constructed using these cellular automatons demonstrating the Turing-completeness of the GoL.
The important thing to note here is that the automatons in the cells are very simple, and their rules can be easily implemented. Despite this apparent simplicity, the collection of interacting automatons can perform any computation of arbitrary complexity given enough time, a large enough grid, and the correct initial configuration (program).
Rule 110
Despite its simplicity, Conway’s Game of Life is still a bit too complex implement in Minecraft in an afternoon (though, it has been done before). The primary complication is that the GoL is a 2D cellular automaton that needs the state of all eight neighbors and itself to compute its next state. Simpler Turing complete automatons exist, and possibly the simplest is known as Rule 110: a one dimensional automaton that only needs the state of its two neighbors and itself to compute its next state. Like the GoL, the automatons have two states: active (1) and inactive (0). The possible inputs to the automaton can be written as binary numbers where the first digit is the neighbor to the left, the second the current cell, and the third the neighbor to the right. This means there are eight possible inputs, each resulting in the automaton updating to either 0 or 1 as follows:
$$ 111 \rightarrow 0 $$ $$ 110 \rightarrow 1 $$ $$ 101 \rightarrow 1 $$ $$ 100 \rightarrow 0 $$ $$ 011 \rightarrow 1 $$ $$ 010 \rightarrow 1 $$ $$ 001 \rightarrow 1 $$ $$ 000 \rightarrow 0 $$
Why is it called “Rule 110”? All possible 1D automatons that take nearest neighbor states as input can be written out in the same fashion, but with different next states. The sequence of next states (with the inputs in the order given) is unique for a particular automaton of this class, and is $01101110$ for this automaton. $01101110$ interpreted as a binary number has the base-10 value 110.
Alternatively, if the state of the automaton to the left is represented by value $a$, the center automaton state being $b$, and the state of the automaton to the right being $c$, the next state of center automaton is given by the C-syntax expression:
(a && b && c) != (b || c)
This will be useful later when implementing this automaton in Minecraft redstone.
Universality of Rule 110
Much like the Game of Life, Rule 110 automatons support translating patterns (again, “spaceships” or “gliders”), now just in 1D instead of 2D. These patterns can interact to transform into other patterns, destroy each other, or delay the translation. As before, these interactions can be exploited to construct Turing complete logical machines, proving Turing completeness of Rule 110. This was done by Matthew Cook where he also outlines the possible gliders available in this automaton.
Minecraft redstone
Minecraft (vanilla Minecraft, even!) has its own Turing-complete set of blocks based around an energy-conducting substance known as “redstone”. There are two key elements to a redstone system:
- Redstone wire, which conducts redstone energy from place to place.
- Redstone torches, which emit redstone energy to adjacent redstone wires.
In the game, redstone energy can be used to “activate” certain other blocks, such as lights, pistons, or doors.
It can also be emitted by yet more blocks, such as player-detecting pressure plates, causing actions in-game.
Redstone Redstone 
NOT gate with input OFF
NOT gate with input ONOFF (emit no energy) if they are attached to an energized block (a block receiving redstone energy, ON).
This results in a NOT gate: a logical inversion of the input state.
An OR gate requires nothing special: since the output should be ON when any of the inputs are ON, a redstone wire can simply aggregate the inputs into the output.
This is all we really need to construct any boolean logic we might need.
An AND gate (a && b) can be constructed with the relationship:
!( !a || !b )
while an XOR (a != b) is only a bit more complicated:
!( !(a||b) || a ) || !( !(a||b) || b )

Redstone XOR gate with one input ON
In fact, any logical operation can be built from these operations. The real trick, much like with designing integrated circuits or PCBs, is figuring out how to lay out the redstone blocks to implement the desired logical operations, which in this case is the Rule 110 expression.
Rule 110 in redstone
In addition to implementing the Rule 110 logical operation for the next state:
(a && b && c) != (b || c)
the 1D cellular automatons will require a mechanism for buffering the next state output and recursively loading it back into the redstone circuitry along with some tessellating pattern to transfer the current state left and right to neighboring automatons.
The final design is given below:
 Though an annotated version will help clarify what’s going on:
Though an annotated version will help clarify what’s going on:
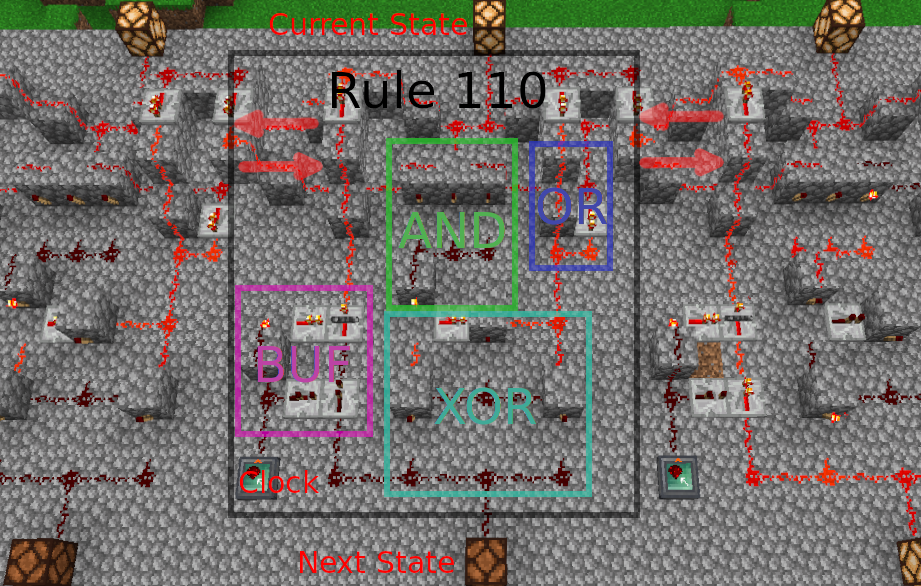 Beyond what was already described, there are two additional details that make this easier to build.
First, there are discrete (vanilla) blocks called redstone repeaters, which are essentially two
Beyond what was already described, there are two additional details that make this easier to build.
First, there are discrete (vanilla) blocks called redstone repeaters, which are essentially two NOT gates compressed into one block.
These act as a diode (one way signal path) and also amplify the redstone signal to value 15 (redstone signals decay by one analog unit per block traveled), and are very useful for creating compact designs.
These repeaters will also hold the output if another repeater applies a signal to their side, as can be seen in the BUF part of the diagram, which allows a clock signal to transfer the next state into the current state.
This clock is distributed with a special block from the RFTools mod called a redstone transmitter, which allows for instantaneous transmission of a redstone signal from a receiver (not shown) to all transmitters paired with it.
Otherwise, redstone signals propagate at one block per “tick” (20 ticks per second), which would make for a slow rolling update if the clock were distributed with vanilla redstone wires.
In vanilla Minecraft (assuming you’re not cheating), this automaton cell would have to be built by hand over and over again many times to achieve enough cells to perform some useful computation. In modded Minecraft there are many options for tools to wholesale copy the cells, making this a much more achievable task. Perhaps I will follow up this post with a large enough number of cells to do some useful Rule 110 demonstration, but as of writing this post I only have dozens constructed.
Why cellular automatons, though?
One might wonder why bother creating a cellular automaton in Minecraft, but I think that’s a silly question; cellular automatons are cool, and so is Minecraft! Cellular automatons (perhaps unlike Minecraft) also have much broader application to the real world. In a sense, it is much easier to build a larger system from many identical subunits than it is to directly construct some very large and complicated machine. This is as true in Minecraft as it is in biology, where all life is constructed from (nominally very similar) biological cells. Further, there are parallels between the emergent properties of cellular automatons (“gliders” or “spaceships”) and our current understanding of particle physics have striking parallels. Both computation in cellular automatons and physics in the universe can be described as the interaction of a finite set of particles that obey universal rules. In fact, the difference between cellular automatons and lattice field theories is mostly in the nature of the number and nature of rules, states, and dimensions chosen for each cell. This idea is still in the earliest stages of being explored, though notable scientists like Gerard ’t Hooft have explored quantum physics from a perspective of cellular automatons, and cellular automaton physics remains a topic of interest and vague speculation for Stephen Wolfram. These ideas are certainly controversial, but the similarities between particle physics and cellular automaton computation are hard to ignore!
>> Home